【机器学习笔记 - 吴恩达】1-4 机器学习介绍 & 概述 &单变量线性回归 & 线性回归训练
1 Introduction to Machine Learning
机器学习(Machine Learning,ML)是人工智能的一个子领域,其核心思想是构建算法模型,这些模型能够从数据中识别模式和规律。
机器学习主要分为几大类:监督学习(从带标签的数据中学习输入到输出的映射)、无监督学习(在没有标签的数据中发现隐藏结构和模式)和强化学习(通过与环境的交互和奖励机制来学习最优行为)。
2 Machine Learning Overview
2.1 Supervised Learning
监督学习是机器学习中最常见的一种范式。它要求使用带有标签(Label)的数据进行训练。这意味着每个输入数据都对应着正确的输出答案。模型通过学习这对输入-输出之间的映射关系,目标是能够对未见过的新数据进行准确的预测或分类。
回归是监督学习任务中的一类,用于预测连续的数值型输出。例如,预测房屋的价格、明天的气温、股票的走势等。模型的输出是一个连续的数值,而不是一个离散的类别。
分类是监督学习任务中的另一类,用于预测离散的类别标签。例如,判断一张图片是“猫”还是“狗”(二分类),或识别电子邮件是“垃圾邮件”还是“非垃圾邮件”(二分类),以及将新闻文章归类到“体育”或“娱乐”等多个类别(多分类)。
2.2 Unsupervised Learning
无监督学习是另一种机器学习范式,它使用没有标签的数据进行训练。模型的目标是自主探索数据的内在结构、模式或分布规律,而不是学习一个预先定义的输入到输出的映射。它主要用于数据探索和降维。
聚类(Clustering)是无监督学习中最常见的任务。它的目的是将数据点自动分组,使得同一组内的数据点(即一个“簇”或“集群”)彼此之间相似度高,而不同组之间的数据点相似度低。聚类常用于市场细分(将客户划分为不同群体)和图像分割。
异常检测 (Anomaly Detection)也称离群点检测,是一种旨在识别数据集中罕见事件、观测值或模式的任务,这些事件与绝大多数数据点的行为显著不同。例如,识别信用卡交易中的欺诈行为、设备运行中的故障指标或网络入侵活动。异常点通常代表着重要的信息或问题。
3 Linear Regression with One Variable
3.1 Linear Regression Model
定义一些常用记号:
- xxx表示输入的变量,也叫“特征”(feature)
- yyy表示输出的变量,或目标变量
- y^\hat yy^表示模型的预测值,读作 y hat
- mmm表示训练样本的数量(训练集的大小)
- (x,y)(x, y)(x,y)表示一个训练样本
对于最简单的单变量线性回归,目标是拟合这样这个线性函数:
fw,b(x)=wx+bf_{w, b}(x) = wx+bfw,b(x)=wx+b
3.2 Cost Function
训练线性回归模型的关键是定义一个成本函数(或者叫代价函数,Cost Function),衡量模型预测值与真实值之间差异的函数
最常用的是均方误差(Mean Squared Error,MSE)函数,计算所有训练样本的预测误差的平方的平均值。通过最小化这个成本函数的值,我们可以找到最佳的模型参数,使得模型的预测尽可能地接近真实数据。
J(w,b)=12m∑i=1m(y^(i)−y(i))2=12m∑i=1m(fw,b(x(i))−y(i))2\begin{aligned} J(w, b) &= \frac 1 {2m} \sum_{i=1}^{m}(\hat y^{(i)} - y^{(i)})^2 \ &= \frac 1 {2m} \sum_{i=1}^{m}(f_{w, b}(x^{(i)}) - y^{(i)})^2 \end{aligned}J(w,b)=2m1i=1∑m(y^(i)−y(i))2=2m1i=1∑m(fw,b(x(i))−y(i))2
注:这里的分母是2m而不是m,实际上都可以,但是2m有利于后续约分,之后介绍。
4 Training Linear Regression
4.1 Gradient Descent
梯度下降是最小化成本函数的一种常见方法,基本做法是:
- 初始化w, b的值(一般都设为0即可)
- 通过对成本函数分别对w和b取偏导,然后向成本函数减小的方向移动一小段距离
- 重复步骤2(通常是设置确定的重复次数),达到成本函数的某个局部最小值
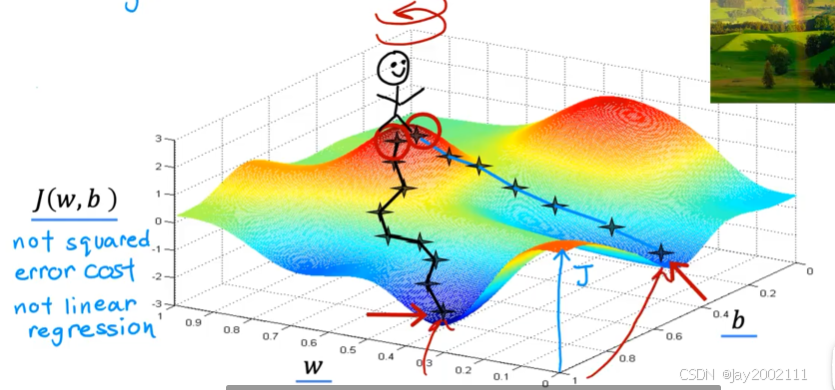
注:可能有不止一个局部最小值
4.2 Implementation Gradient Descent
用表达式表示梯度下降的过程:
w=w−α∂∂wJ(w,b)b=b−α∂∂bJ(w,b)
\begin{aligned}
w &= w - \alpha \frac {\partial} {\partial w} J(w, b) \
b &= b - \alpha \frac {\partial} {\partial b} J(w, b)
\end{aligned}wb=w−α∂w∂J(w,b)=b−α∂b∂J(w,b)
注:
- 这里的α\alphaα称作学习率(Learning Rate)
- w和b的值要同步更新,否则先改变了w,会影响b的赋值语句的右边表达式的值

4.3 Gradient Descent Intuition
梯度下降的原理可以想象成一个人蒙着眼睛从山顶走到山谷底部的过程。他每一步都会朝当前位置最陡峭的下坡方向迈进(偏导),这个最陡峭的方向就是“负梯度”的方向。每一步迈出的“步子大小”由学习率控制,确保既能快速接近谷底,又不会因为步子太大而跳过局部最低点(即成本函数的局部最小值)。通过不断迭代地沿着负梯度方向更新模型参数,算法最终会收敛到成本函数局部最低点的附近。
4.4 Learning Rate
- 学习率大会导致“步子”迈得过大,可能直接跳过最优解,使成本函数剧烈震荡甚至发散,难以收敛
- 学习率小则会导致“步子”太小,收敛过程极其缓慢,浪费大量时间
- 在凸优化问题中(如基础线性回归),成本函数只有一个全局最低点,当接近谷底时,梯度会自动变小,即使学习率不变,参数更新的幅度也会随之减小,因此学习率保持不变也能让模型平稳地收敛到最低点附近
4.5 Gradient Descent for Linear Regression
先看成本函数公式:
J(w,b)=12m∑i=1m(fw,b(x(i))−y(i))2=12m∑i=1m(wx(i)+b−y(i))2J(w, b) = \frac 1 {2m} \sum_{i=1}^m (f_{w, b}(x^{(i)}) - y^{(i)})^2 = \frac 1 {2m} \sum_{i=1}^m (wx^{(i)}+b - y^{(i)})^2J(w,b)=2m1i=1∑m(fw,b(x(i))−y(i))2=2m1i=1∑m(wx(i)+b−y(i))2
对w求偏导:
∂∂wJ(w,b)=12m∑i=1m2⋅x(i)⋅(wx(i)+b−y(i))=1m∑i=1mx(i)⋅(wx(i)+b−y(i))=1m∑i=1m(fw,b(x(i))−y(i))x(i)\begin{aligned}
\frac {\partial} {\partial w} J(w, b) &= \frac 1 {2m} \sum_{i=1}^{m}2 \cdot x^{(i)} \cdot (wx^{(i)}+b-y^{(i)}) \
&= \frac 1 m \sum_{i=1}^{m}x^{(i)} \cdot (wx^{(i)}+b-y^{(i)}) \
&= \frac 1 m \sum_{i=1}^{m} (f_{w, b}(x^{(i)})-y^{(i)})x^{(i)}
\end{aligned}∂w∂J(w,b)=2m1i=1∑m2⋅x(i)⋅(wx(i)+b−y(i))=m1i=1∑mx(i)⋅(wx(i)+b−y(i))=m1i=1∑m(fw,b(x(i))−y(i))x(i)
对b求偏导:
∂∂bJ(w,b)=12m∑i=1m2⋅(wx(i)+b−y(i))=1m∑i=1m(wx(i)+b−y(i))=1m∑i=1m(fw,b(x(i))−y(i))\begin{aligned}
\frac {\partial} {\partial b} J(w, b) &= \frac 1 {2m} \sum_{i=1}^{m} 2 \cdot (wx^{(i)}+b-y^{(i)}) \
&= \frac 1 m \sum_{i=1}^{m} (wx^{(i)}+b-y^{(i)}) \
&= \frac 1 m \sum_{i=1}^{m} (f_{w, b}(x^{(i)})-y^{(i)})
\end{aligned}∂b∂J(w,b)=2m1i=1∑m2⋅(wx(i)+b−y(i))=m1i=1∑m(wx(i)+b−y(i))=m1i=1∑m(fw,b(x(i))−y(i))
代入梯度下降公式:
w=w−α1m∑i=1m(fw,b(x(i))−y(i))x(i)b=b−α1m∑i=1m(fw,b(x(i))−y(i))\begin{aligned}
w &= w - \alpha \frac 1 m \sum_{i=1}^{m} (f_{w, b}(x^{(i)})-y^{(i)})x^{(i)} \
b &= b - \alpha \frac 1 m \sum_{i=1}^{m} (f_{w, b}(x^{(i)})-y^{(i)})
\end{aligned}wb=w−αm1i=1∑m(fw,b(x(i))−y(i))x(i)=b−αm1i=1∑m(fw,b(x(i))−y(i))
4.6 Running Gradient Descent
Batch Gradient Descent(BGD):整个数据集每次参数更新都使用整个训练数据集来计算梯度
还有其他版本的梯度下降,小批量梯度下降(Mini-Batch Gradient Descent,MBGD):每次用一部分数据集,设置Batch Size(批量大小)来控制